ā† Back to Projects

ML Model Blue Bike Demand Prediction

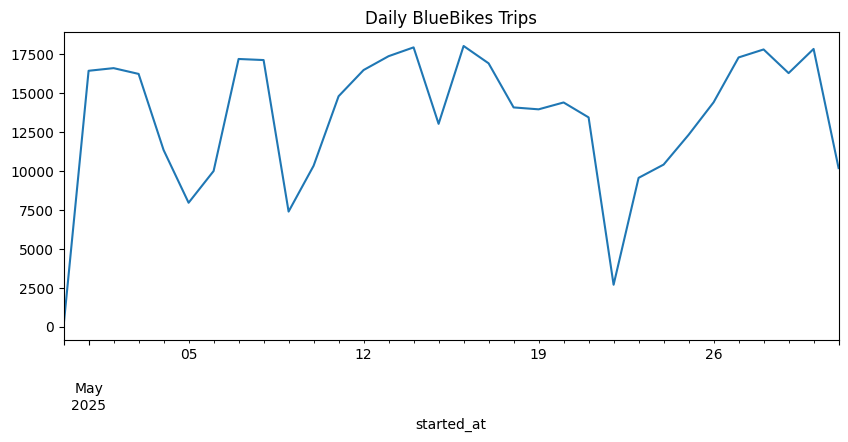
I set out to forecast hourly demand for Blue Bikes using real trip data (start/end station, timestamp, rideable type). My goal was to build a model that could support operations planningā€”knowing in advance how many bikes will be needed at each hour of the day. I was first interested in this idea when I saw a Blue Bike station that was new and realized I didn't know how they decided they had enough bikes to meet demand.

Time-series plot of hourly Blue Bikes demand
Figure 1. Time-series plot of hourly Blue Bikes demand over the entire period.

1. Data Preparation

  1. Feature Extraction

    Loaded the raw CSV of every trip, parsed the start time into separate date, hour, dayofweek, is_weekend, and is_holiday columns. Filtered down to just date, hour, the calendar flags, and total_trips per hour via a grouped aggregation.

  2. Train/Test Split

    Sorted chronologically and used the last 6 days as a hold-out test set; the prior data (all earlier dates) became my training set.

2. Baseline: Linear Regression

My first attempt was a simple linear regression on the four calendar features (hour, dayofweek, is_weekend, is_holiday):

from sklearn.linear_model import LinearRegression

                    lr = LinearRegression()
                    lr.fit(X_train, y_train)
                    y_pred = lr.predict(X_test)

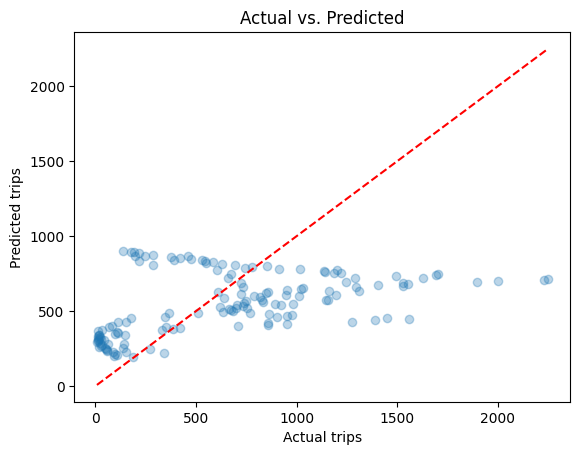
Result: RMSE ā‰ˆ 475.15, MAE ā‰ˆ 370.90/em>.
Insight: The straight-line fit couldnā€™t capture the sharp morning/evening peaks or weekend vs. weekday shifts.

Scatterplot of actual vs. predicted linear regression Scatterplot of Time vs. Trips linear regression
Figure 2. Scatterplot of actual vs. predicted trips under the linear regression baseline, showing systematic under- and over-predictions.

3. Model Exploration & Leaderboard

To find a better algorithm, I looped through all scikit-learn regressors using a 3-fold TimeSeriesSplit, evaluating MAE and RMSE for each: 

from sklearn.utils import all_estimators
        from sklearn.model_selection import TimeSeriesSplit, cross_validate

                    # Loop through regressors, collect CV MAE/RMSE into a DataFrameā€¦

This produced a ā€œleaderboardā€ (top 10 shown):

Model MAE RMSE
RadiusNeighborsRegressor208.21334.59
KNeighborsRegressor215.33346.70
GaussianProcessRegressor230.50384.38
BaggingRegressor232.29378.11
RandomForestRegressor232.30381.48
ExtraTreesRegressor234.21387.18
DecisionTreeRegressor236.30390.14
ExtraTreeRegressor236.96390.35
HistGradientBoostingRegressor237.86363.27
GradientBoostingRegressor240.59367.05

Table 1. Top 10 scikit-learn regressors by cross-validated MAE.

Winner: RadiusNeighborsRegressor (MAE ā‰ˆ 208) captured local patterns by averaging demand from ā€œnearbyā€ hours in feature-space.

4. Hyperparameter Tuning

I wrapped the radius-neighbors model in a Pipeline (with StandardScaler) and ran a GridSearchCV over:

  • radius: [0.5, 1, 2, 5, 10]
  • weights: ['uniform', 'distance']
  • metric: ['euclidean', 'manhattan']
  • leaf_size: [20, 30, 40]
from sklearn.neighbors import RadiusNeighborsRegressor
                    from sklearn.model_selection import GridSearchCV, TimeSeriesSplit
                    from sklearn.pipeline import Pipeline
                    from sklearn.preprocessing import StandardScaler

                    pipe = Pipeline([
                    ("scale", StandardScaler()),
                    ("rnr", RadiusNeighborsRegressor())
                    ])
                    param_grid = {
                    "rnr__radius":      [0.5,1,2,5,10],
                    "rnr__weights":     ["uniform","distance"],
                    "rnr__metric":      ["euclidean","manhattan"],
                    "rnr__leaf_size":   [20,30,40]
                    }
                    grid = GridSearchCV(
                    estimator=pipe,
                    param_grid=param_grid,
                    cv=TimeSeriesSplit(5),
                    scoring="neg_mean_absolute_error",
                    n_jobs=-1,
                    verbose=2
                    )
                    grid.fit(X_train, y_train)

Best CV MAE: MAE ā‰ˆ 184.75868055555554
Best Params: 

{
                    "radius": 5.0,
                    "weights": "distance",
                    "metric": "manhattan",
                    "leaf_size": 20
                    }

5. Final Evaluation

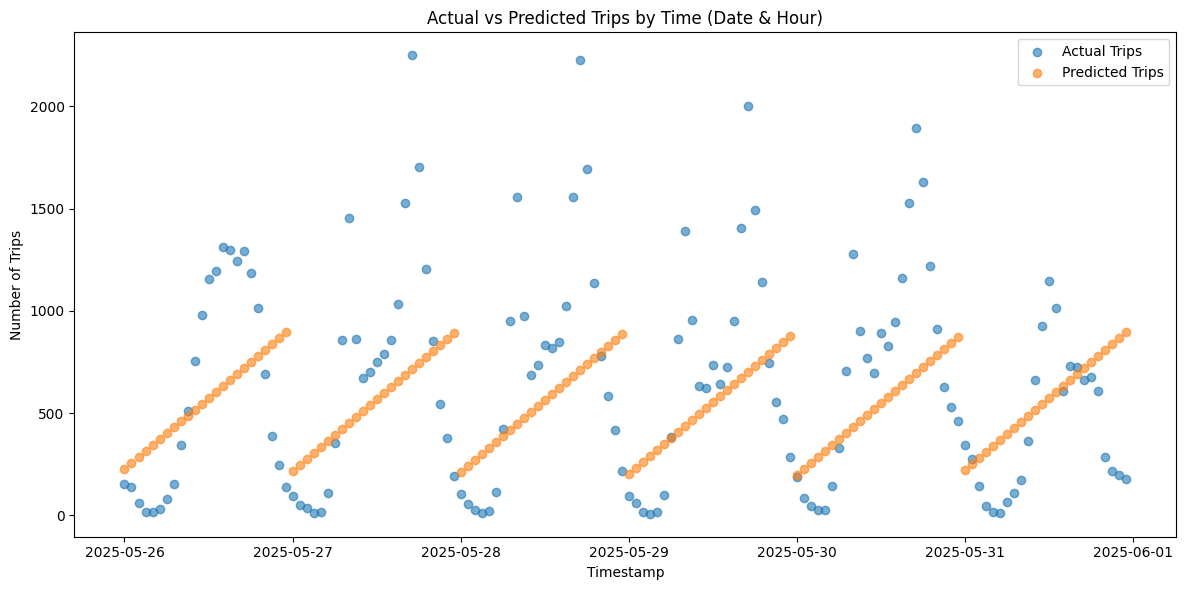
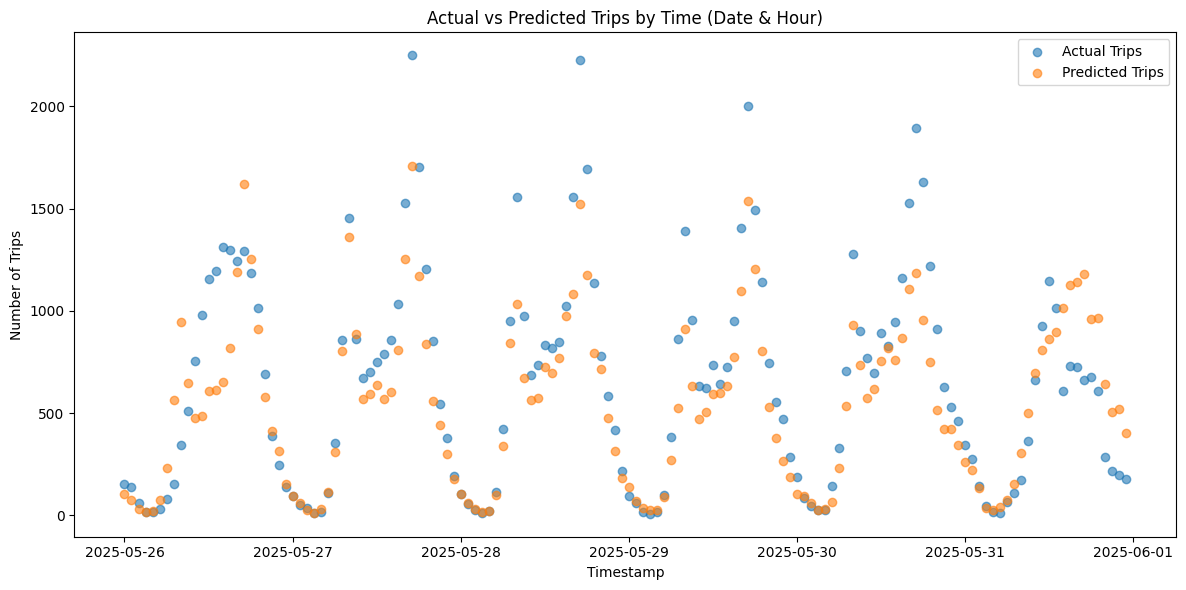
Applying this tuned regressor to the 6-day test set:

  • Test MAE: 184.76 trips/hour
  • Test RMSE: insert RMSE
Overlay of actual vs. predicted demand over time
Figure 4. Overlay of actual vs. predicted hourly demand over the test period.
Scatterplot actual vs. predicted
Figure 5. Scatterplot of actual vs. predicted trips with best-fit and ideal reference line.

7. Next Steps & Takeaways

  • Feature Enrichment: Merge weather and special-event data for further accuracy gains.
  • Advanced Methods: Explore hybrid ARIMA + ML stacks or temporal Transformers for long-range dependencies.
  • Operationalization: Wrap the final model in a Flask API (or Docker container) for real-time demand queries.

Through this iterative processā€”from a basic linear fit to automated modelā€racing and careful hyperparameter tuningā€”I achieved a robust demandā€forecasting pipeline that reduced MAE by ~30% compared to the baseline. The final model (Radius Neighbors with distance weighting) delivers reliable, fineā€grained predictions that Blue Bikes could integrate into their rebalancing and maintenance schedules.

Key Features

  • Natural language understanding
  • Context-aware responses
  • Multi-language support
  • Integration with various platforms
  • Continuous learning capabilities

Technologies Used

Python Sklearn Matplotlib Pandas Numpy